Square divided by four

The scaling factor from one generation to the next is 1/2. This reptile has four-fold rotational symmetry and mirror symmetry, allowing for choices in the orientation of the smaller units in cases where those units have less symmetry than a square. If overall rotations or reflections are not considered distinct, there is one possibility for removing one square in the first iteration. There are 64 possibilities for the second iteration (four rotations for each of three trombones), 36 of which are distinct. Of these, 8 have mirror symmetry and therefore a single possibility for a third iteration, while 28 lack mirror symmetry and therefore have 8 possibilities for a third iteration. The construction rules are fully locked in after three iterations, making the total number of distinct fractals 8 + 28*8 = 232.

Four of the five examples below have mirror symmetry. These are shown on Larry Riddle's page "Sierpinski Relatives". The fifth, lacking mirror symmetry, is not. The examples below are all carried through eight iterations. You may need to widen your browser window in order to see all five columns side by side. The ninth iteration of the fourth gasket from the left is shown at larger scale at the bottom of the page.












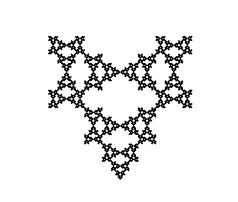
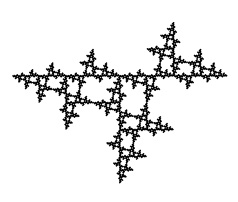
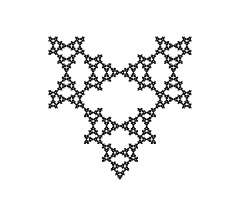
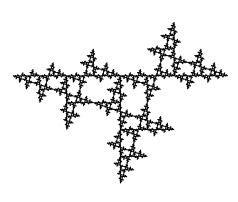
Two spatially-developing fractal-gasket polyhedra based on the second and fourth gaskets above:

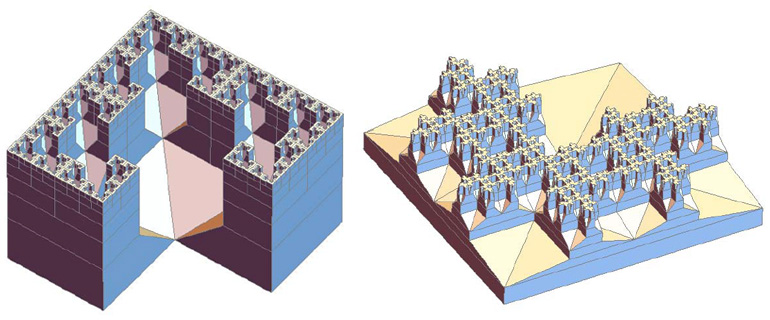
All images copyright Robert Fathauer

Fractal Diversions home

Fractal Tiling Fractal Knots Gasket Fractals Fractal Trees Hyperbolic & Folded Fractals Polyhedra Papers