
Introduction to Fractals
Classical Fractals
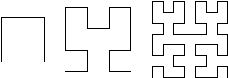
Classical fractals were "mathematical monsters" that defied description. An example is the Hilbert curve, described in a paper dating to 1890. It is a line, so one could consider it a one-dimensional object. On the other hand, it completely fills a portion of the plane, so one could also consider it a two-dimensional object. The Hilbert curve is generated by iteration, which refers to the repeated application of a rule or equation. Iteration is a central concept in fractals, where iterations are carried out an infinite number of times in theory. The first three iterations of the Hilbert curve are shown below.
Modern Fractals
The idea of fractals as a distinct branch of mathematics is largely due to the work of Benoit Mandelbrot. He formalized the concept of fractal dimension, which assigns a dimension between 1 and 2, for example, to the Hilbert curve. He also discovered the unusual properties of the enigmatic Mandelbrot set (shown below), an infinite swarm of points clustered on the complex number plane. This understanding of fractals also allowed earlier work by mathematician Gaston Julia to be used to create similar objects, an example of which is shown below after the Mandelbrot set. Construction of such figures in any detail wouldn't have been possible without modern computers.


Fractals in nature
Many objects in nature exhibit fractal character. An example is the coastline of a continent. As one zooms in for closer and closer looks, the sorts of features one sees (protrusions, indentations, etc.) tend to appear over and over again. This attribute is called self similarity. The self similarity of natural objects is approximate, which that of mathematical constructs can be approximate or exact. Other examples of natural objects with fractal character are a mountain range, the system of arteries in the human body, and the structure of clouds.
© 2000-2015 Tessellations
mathartfun.com home

